支配树算法原理及鸿蒙工具实践
- 2026-02-01 15:52:36


▐⽀配树是什么
 ,如果节点
,如果节点 ⽀配节点
⽀配节点 ,当且仅当从
,当且仅当从 →
→ 的所有路径都经过节点
的所有路径都经过节点 ,记
,记 如果不存在
如果不存在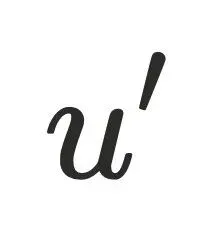 使得
使得 且
且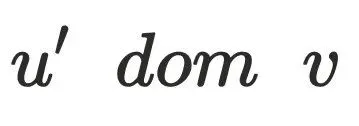 ,则
,则 是
是 的直接⽀配节点,记做
的直接⽀配节点,记做 。从⼊⼝
。从⼊⼝ 通过直接⽀配节点形成的树则称为⽀配树,即⽀配树中每个节点的⽗节点都是其直接⽀配节点。
通过直接⽀配节点形成的树则称为⽀配树,即⽀配树中每个节点的⽗节点都是其直接⽀配节点。classB{int c;}classA{B b = new B();}A a = new A();
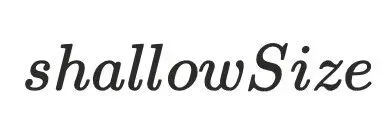 ,指的是对象本身的内存⼤⼩。上⽅代码中,a对象中有⼀个引⽤指针b,
,指的是对象本身的内存⼤⼩。上⽅代码中,a对象中有⼀个引⽤指针b, 为4bytes。b对象中有⼀个变量c,
为4bytes。b对象中有⼀个变量c, 为4bytes
为4bytes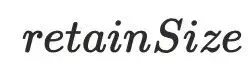 ,指的是回收该对象之后虚拟机能够回收的内存⼤⼩。a对象的
,指的是回收该对象之后虚拟机能够回收的内存⼤⼩。a对象的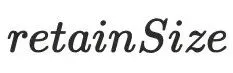 为8,释放a之后可以同时释放b,所以
为8,释放a之后可以同时释放b,所以
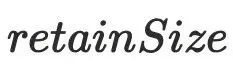 占⽤较⾼的对象回收掉就可以解决内存溢出的问题。如果将对象抽象为有向图中的节点,对象间的引⽤关系则可以抽象为有向图中的边,例如上⾯的代码,a对象引⽤b对象,可以抽象为下图。
占⽤较⾼的对象回收掉就可以解决内存溢出的问题。如果将对象抽象为有向图中的节点,对象间的引⽤关系则可以抽象为有向图中的边,例如上⾯的代码,a对象引⽤b对象,可以抽象为下图。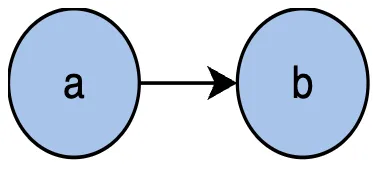
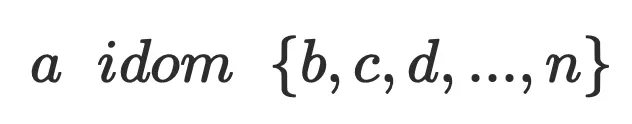 ,根据⽀配树的特性,回收 a对象,
,根据⽀配树的特性,回收 a对象,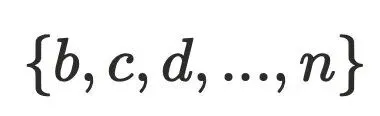 在内存中就成了孤⽴对象可以被GC,由此可以得出:
在内存中就成了孤⽴对象可以被GC,由此可以得出: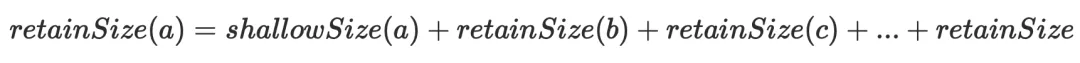
朴素算法,原理是对每个节点  ,依次删除图中的其他节点,判断是否存在路径从根节点到达节点
,依次删除图中的其他节点,判断是否存在路径从根节点到达节点 ,算法复杂度为
,算法复杂度为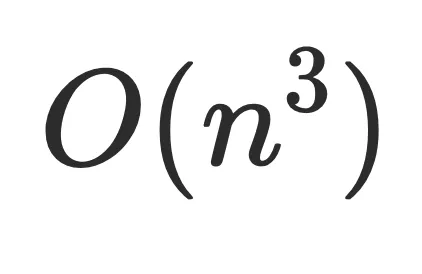 ,复杂度过⾼,⼀般不使⽤。
,复杂度过⾼,⼀般不使⽤。Lengauer-Tarjan算法,经典的⽀配树算法,⼀般情况是 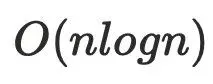 优化后的算法复杂度
优化后的算法复杂度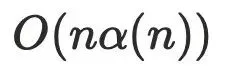 , α 是阿克曼函数,可以理解为趋近于线性
, α 是阿克曼函数,可以理解为趋近于线性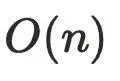 。
。迭代算法,通常是用于在编译器的控制流当中,算法复杂度是 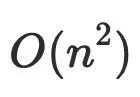 ,优化后算法复杂度
,优化后算法复杂度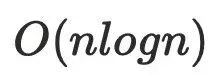 。
。
Lengauer-Tarjan算法原理及其优化⽐较复杂,⼯具类对于构建⽀配树的速度要求没有那么⾼; 可以使⽤华为已实现的profiler插件以及chrome的开源代码作为对⽐,防⽌算法出错; 在内存对象的引⽤关系中,存在很多循环引⽤,节点与节点之间的环⽐较严重,这让Lengauer-Tarjan算法在计算半⽀配节点的时候算法复杂度⼤⼤增加。


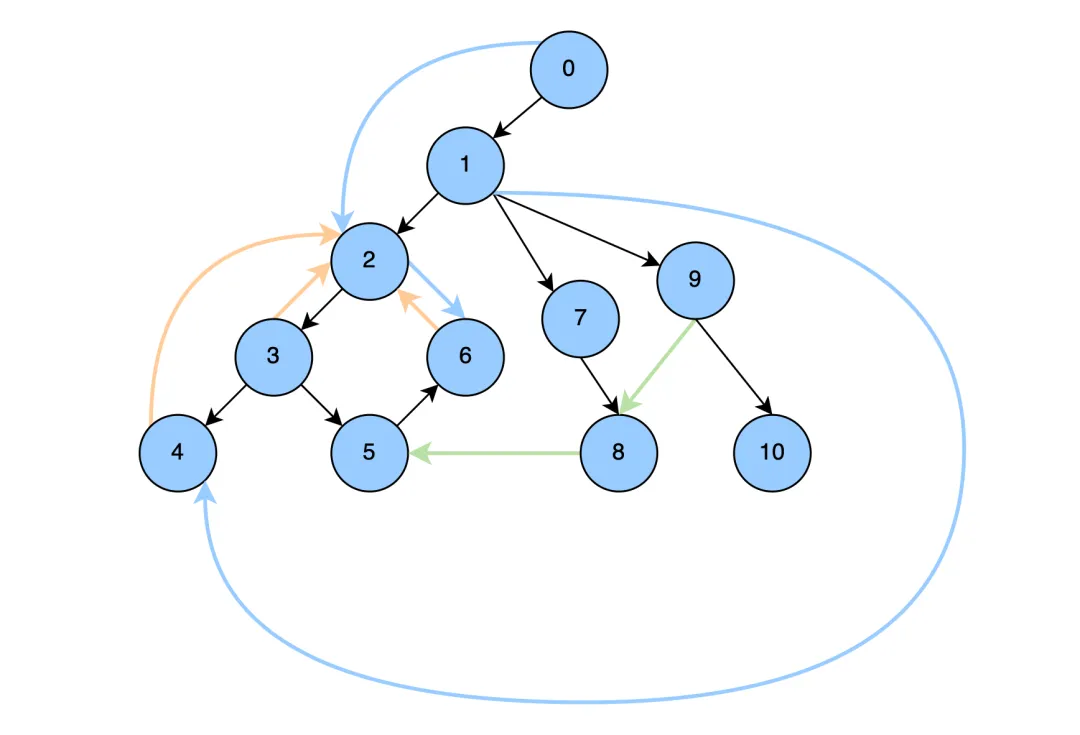
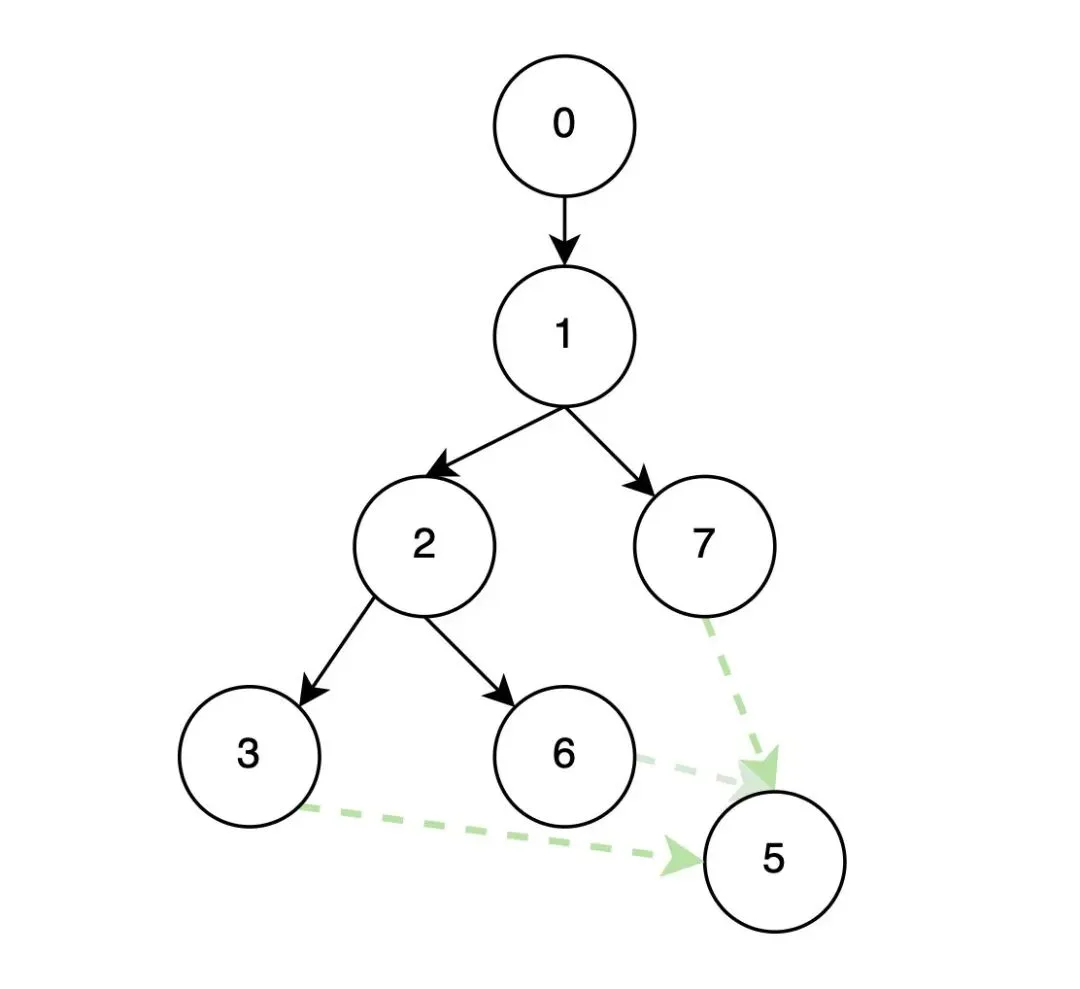
树边,即DFS过程中建⽴的边,在下图中显示为⿊⾊; 前向边,即祖先节点到⼦树⾮⼉⼦的边,在下图中显示蓝⾊, 2->6,1->4,0->2; 返祖边,即节点到祖先节点的变,在下图中显示为橙⾊,4->2,3->2,6->2; 横叉边,即从⾮⼦树、⾮祖先横叉过来的边,在下图中显示为绿⾊,8->5,9->8。
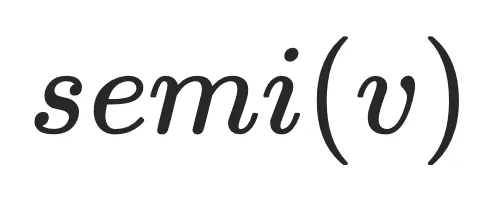 的定义:
的定义:对于任意节点
,如果存在一个节点
,且
的路径中所有节点
(
节点可以不存在)的序号都大于
,则
是
的半支配候选,其中dfs序最小的
被称为
的半支配节点。
 的半⽀配节点可以理解为是通过这四种边到达
的半⽀配节点可以理解为是通过这四种边到达 最远祖先节点(⽐当前节点dfs序⼩的节点只有可能是祖先节点或者左⼦树节点,dfs必须遍历完左⼦树再遍历右⼦树,左⼦树节点不可能存在到右⼦树节点的边,只可能是祖先节点)。由半⽀配节点的定义可得:
最远祖先节点(⽐当前节点dfs序⼩的节点只有可能是祖先节点或者左⼦树节点,dfs必须遍历完左⼦树再遍历右⼦树,左⼦树节点不可能存在到右⼦树节点的边,只可能是祖先节点)。由半⽀配节点的定义可得:⽗节点是半⽀配候选,例如: 3->5 前向边的节点是半⽀配候选,例如:2->6 返祖边的节点是半⽀配候选,例如:1->4->2 横叉边的节点是半⽀配者选,例如: 1->7->8->5
 的直接⽀配者,更进⼀步,从半⽀配候选增加⼀条边指向
的直接⽀配者,更进⼀步,从半⽀配候选增加⼀条边指向 不改变
不改变 的⽀配关系,于是对于任意节点
的⽀配关系,于是对于任意节点 ,都可以简化为下⾯的连接关系,其中
,都可以简化为下⾯的连接关系,其中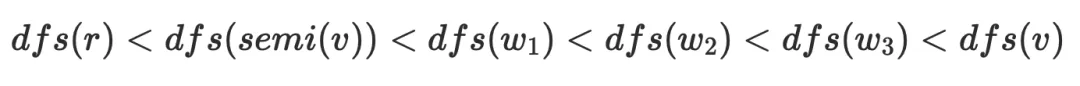
隐含的结论: 半⽀配候选都是在
的树边上
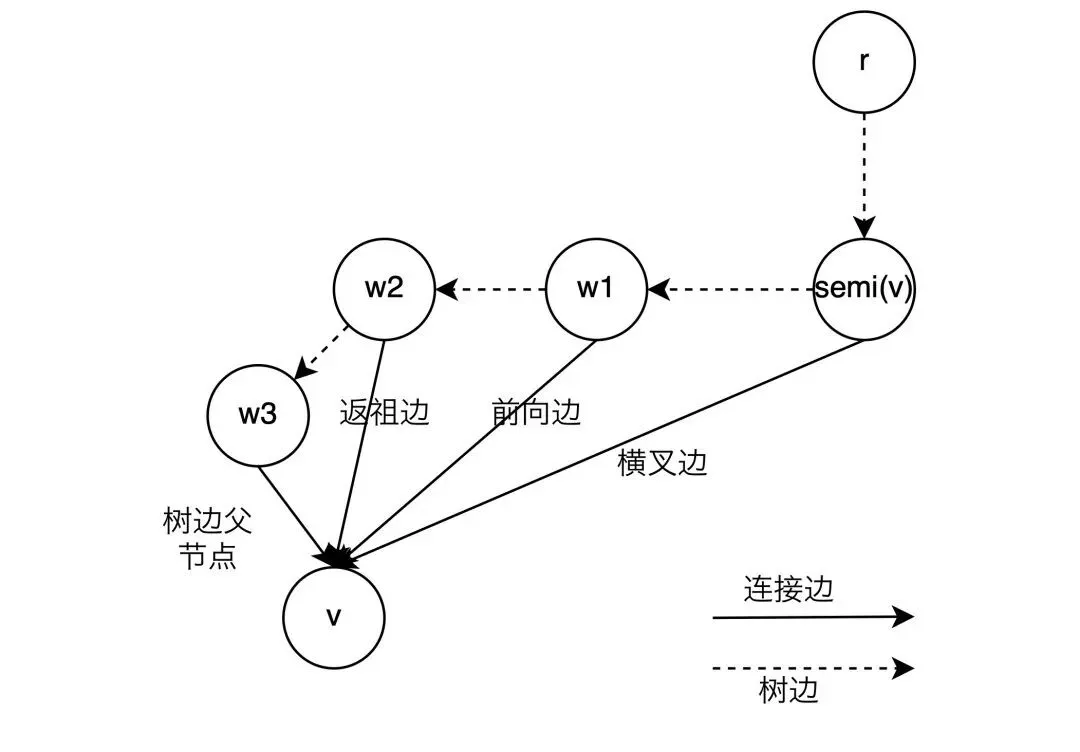
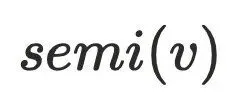 还不能直接⽀配节点,因为还不⽀配
还不能直接⽀配节点,因为还不⽀配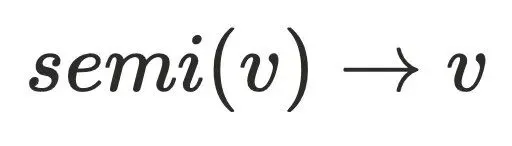 的树边,例如上⾯的dfs序为5的节点,它存在树边(3->5)和横叉边(1->7->8->5),通过定义可以算出它的半⽀配节点
的树边,例如上⾯的dfs序为5的节点,它存在树边(3->5)和横叉边(1->7->8->5),通过定义可以算出它的半⽀配节点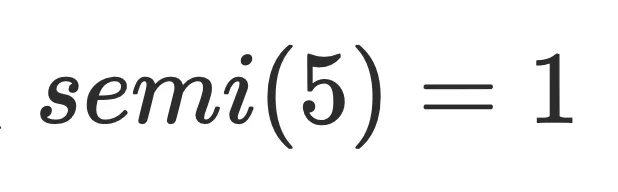 。但实际上还存在0->2->3->5这条路径不经过1号节点,实际上
。但实际上还存在0->2->3->5这条路径不经过1号节点,实际上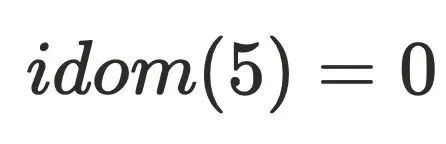 。
。 节点所有中间节点
节点所有中间节点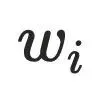 的
的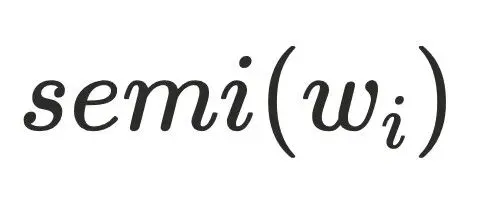 的最⼩dfs序
的最⼩dfs序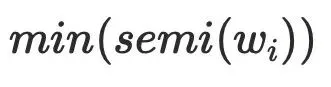 。
。
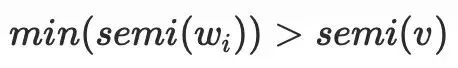 ⽐较好推导,说明不存在有
⽐较好推导,说明不存在有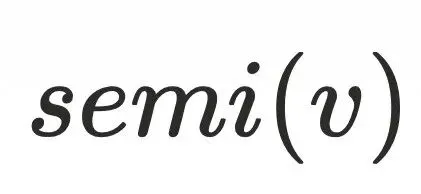 的祖先节点不通过
的祖先节点不通过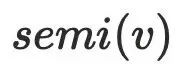 到达
到达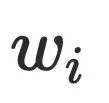 ,⼜由于半⽀配集合都是处于
,⼜由于半⽀配集合都是处于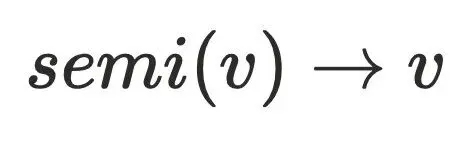 的树边上,所以到达半⽀配集合都得通过
的树边上,所以到达半⽀配集合都得通过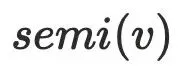 ,故
,故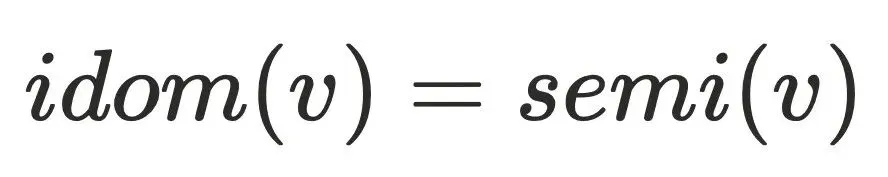
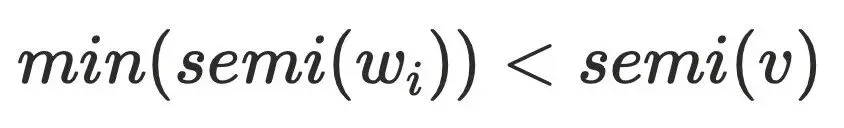 说明⾄少存在⼀个节点
说明⾄少存在⼀个节点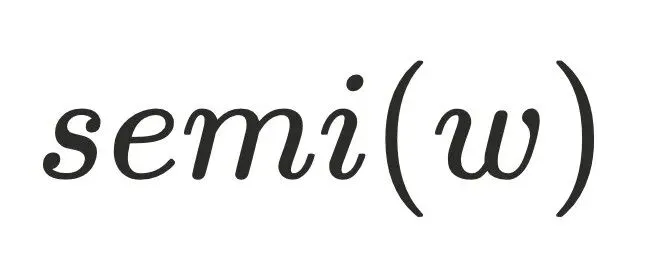 不通过
不通过 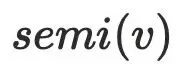 可以到达节点
可以到达节点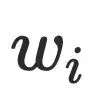 ,其中
,其中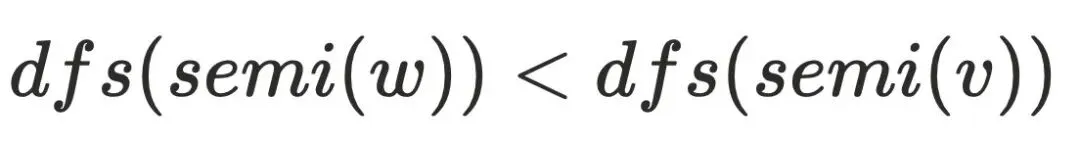 ,可以证明
,可以证明 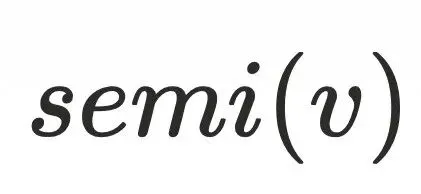 不⽀配
不⽀配 ,可以⼤致得到下图的节点关系,最主要问题是为何不需要考虑其他
,可以⼤致得到下图的节点关系,最主要问题是为何不需要考虑其他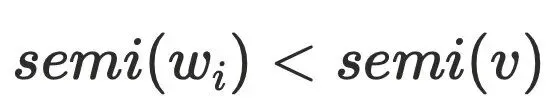 的情况,例如:
的情况,例如: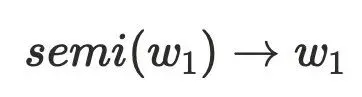 。可以假设
。可以假设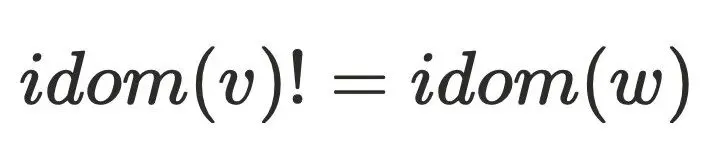 ,则存在
,则存在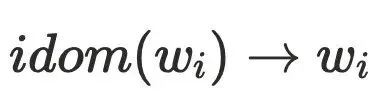 不经过
不经过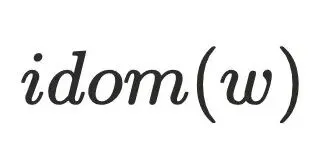 到达
到达 ,但是该条路径必须经过
,但是该条路径必须经过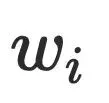 的半⽀配候选集,根据前⾯半⽀配节点隐含的结论,
的半⽀配候选集,根据前⾯半⽀配节点隐含的结论,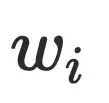 的半⽀配候选集都在
的半⽀配候选集都在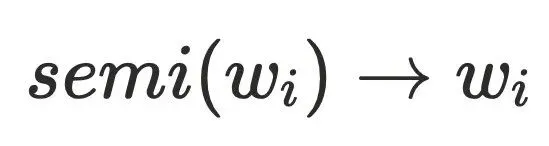 的树边上,且
的树边上,且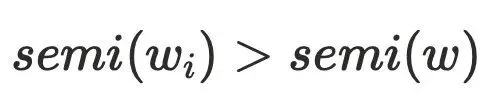 ,由于
,由于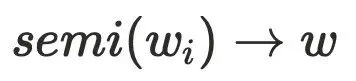 存在树边到达
存在树边到达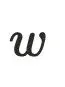 ,这与
,这与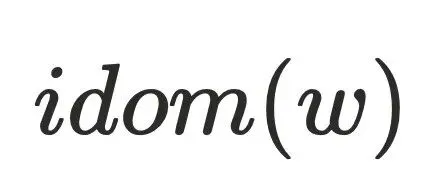 的定义相悖,故
的定义相悖,故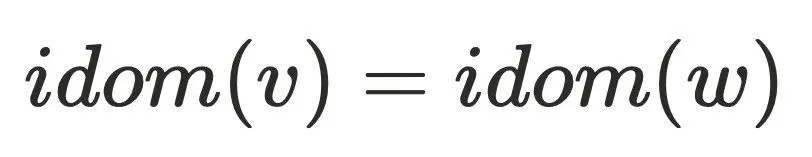 。
。
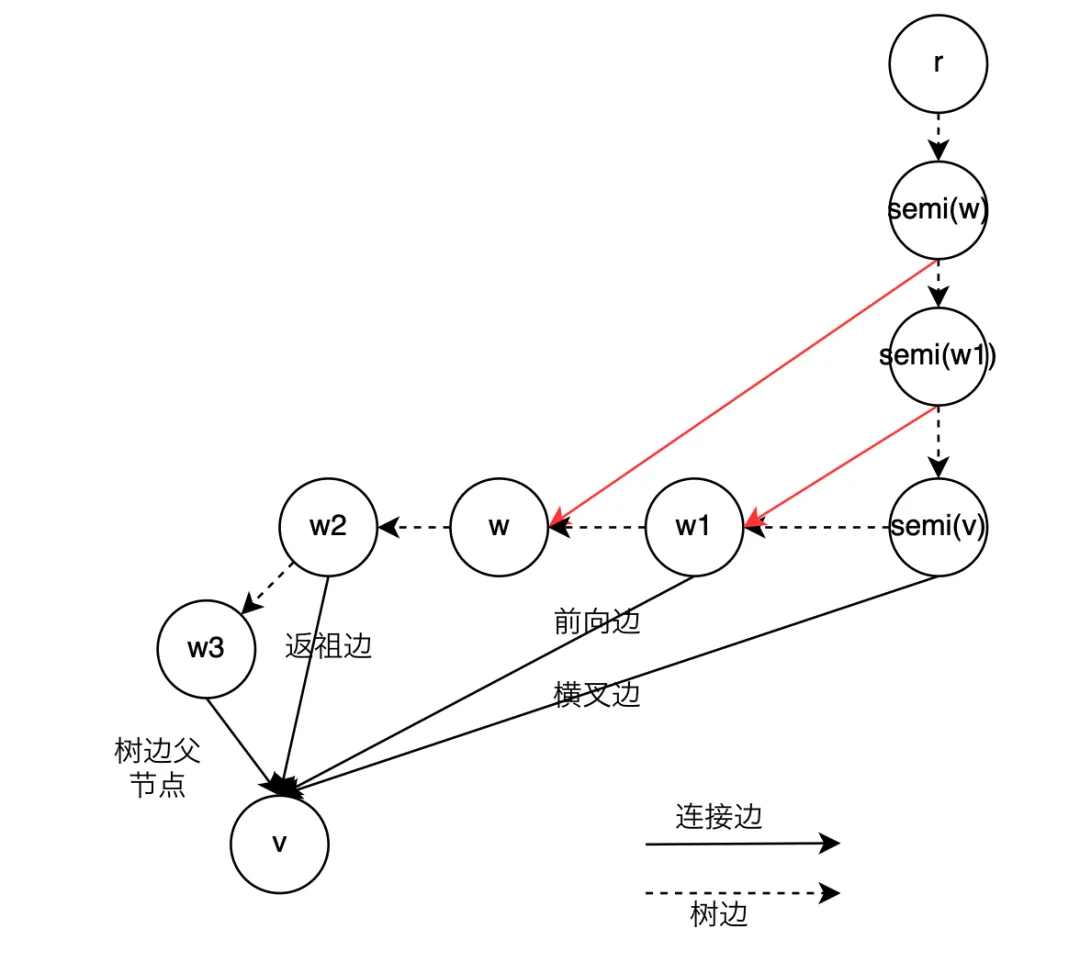

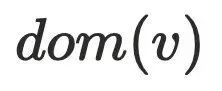 ⽀配节点当且仅当⽀配其前驱节点
⽀配节点当且仅当⽀配其前驱节点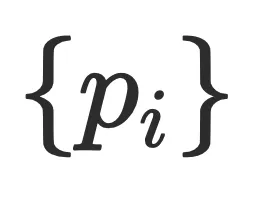 ,简要⽤公式表达:
,简要⽤公式表达: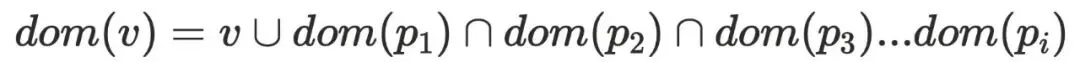
1. 初始化根节点 s , Dom(s) = {s}
2. 初始化其他节点 n , Dom(n) = {全集}
3. 对于⾮根节点 n , Dom(n) = n ∪ (∩Dom(p)) ,即当前节点 n 并上所有前驱节点 p的⽀配节点的交集
4. 重复步骤3,直到所有的 Dom(n) 不再变化
{"snapshot":{"meta":{"node_fields":["type","name","id","self_size","edge_count","trace_node_id","detachedness","native_size"],"node_types":[["hidden","array","string","object","code","closure","regexp","number","native","synthetic","concatenatedstring","slicedstring","symbol","bigint"],"string","number","number","number","number","number"],"edge_fields":["type","name_or_index","to_node"],"edge_types":[["context","element","property","internal","hidden","shortcut","weak"],"string_or_number","node"],"trace_function_info_fields":[...],"trace_node_fields":[...],"sample_fields":[...],"location_fields":[...]},"node_count":100056,"edge_count":384773,"trace_function_count":0},"nodes":[...],"edges":[...],"trace_function_infos":[],"trace_tree":[],"samples":[],"locations":[],"strings":[...],}
meta:定义了节点和边的结构 node_fields:定义了单个内存节点(node)的属性 node_types:内存节点(node)的类型 edge_fields:定义了单个边(edge)的属性 edge_types:定义了边的类型 node_count:节点数量 edge_count:边的数量 nodes:节点的集合 edges:边的集合 strings:所有的字符串,包括边的名称,内存节点的名称等等
内存节点node
"node_fields":["type","name","id","self_size","edge_count","trace_node_id","detachedness","native_size"],"nodes":[9,11693,1,0,6386,0,0,0,8,11696,3,48,1,0,0,0,8,11696,5,48,1,0,0,0,...]
type: 9, //节点类型的偏移name: 11693, //节点名字,大概率是文件名,对应strings中的indexid: 1, //无特殊含义,节点的标号self_size: 0, //大概率是shallow_size,0大概率是数组edge_count: 6386, //跟其他内存节点的引用关系
"node_types":[["hidden","array","string","object","code","closure","regexp","number","native","synthetic","concatenatedstring","slicedstring","symbol","bigint"],"string","number","number","number","number","number"],
引⽤关系edge
"edge_fields":["type","name_or_index","to_node"],"edges":[5,11673,527080,5,11673,527072,5,11673,527056,...]
"edge_types":[["context","element","property","internal","hidden","shortcut","weak"],"string_or_number","node"],context //暂时没有用处element //DOMTree中的元素property //类当中的属性internal //内部属性hidden //隐藏属性shortcut //和property中差不多,通过赋值得到的引用weak //弱引用
name or__index存储的是strings中的名字index,11673对应的是-subroot-字符串to_node代表的是这条边指向的节点索引,因为内存引用构成是一个有向图,所以还需要知道这条边来自于哪个节点。边属于哪个节点的计算是通过内存节点索引+边来进行计算的,举个例子:如果一个节点的序号是0,有10条边,那么edges[0,10)就是属于节点0的,如果序号1的节点有5条边,那么edges[10,15)就是属于节点1的。
privatevoidbuildEdgeIndexes() {firstEdgeIndexes[nodeCount] = edges.length;int nodeOrdinal = 0;for (int edgeIndex = 0; nodeOrdinal < nodeCount; ++nodeOrdinal) {firstEdgeIndexes[nodeOrdinal] = edgeIndex;//nodes[nodeOrdinal * nodeFieldCount + nodeEdgeCountOffset]当前节点持有边的个数edgeIndex += nodes[nodeOrdinal * nodeFieldCount + nodeEdgeCountOffset] * edgeFieldsCount;}}
int edgeLength = edges.length;for (int edgeToNodeIndex = edgeToNodeOffset; edgeToNodeIndex < edgeLength; edgeToNodeIndex += edgeFieldsCount) {int toNodeIndex = edges[edgeToNodeIndex];if (toNodeIndex % nodeFieldCount != 0) {TBPLogger.error("Invalid toNodeIndex is {}", new Object[] {toNodeIndex});} else {int toNodeOrdinal = toNodeIndex / nodeFieldCount;if (isValid(toNodeOrdinal, firstRetainerIndex.length)) {firstRetainerIndex[toNodeOrdinal]++;}}}
int firstUnusedRetainerSlot = 0;for (int nodeOrdinal = 0; nodeOrdinal < nodeCount; ++nodeOrdinal) {int retainerCount = firstRetainerIndex[nodeOrdinal];firstRetainerIndex[nodeOrdinal] = firstUnusedRetainerSlot;if (isValid(firstUnusedRetainerSlot, edgeCount)) {retainingNodes[firstUnusedRetainerSlot] = retainerCount;firstUnusedRetainerSlot += retainerCount;}}
for (srcNodeOrdinal = 0; srcNodeOrdinal < nodeCount; ++srcNodeOrdinal) {firstEdgeIndex = nextNodeFirstEdgeIndex;nextNodeFirstEdgeIndex = firstEdgeIndexes[srcNodeOrdinal + 1];srcNodeIndex = srcNodeOrdinal * nodeFieldCount;for (int edgeIndex = firstEdgeIndex; edgeIndex < nextNodeFirstEdgeIndex; edgeIndex += edgeFieldsCount) {int index = edgeIndex + edgeToNodeOffset;if (isValid(index, edges.length)) {int toNodeIndex = edges[index];if (toNodeIndex % nodeFieldCount != 0) {TBPLogger.error("Invalid toNodeIndex is {}.", new Object[]{toNodeIndex});} else if (isValid(toNodeIndex / nodeFieldCount, firstRetainerIndex.length)) {//retainningNodes的起点int firstRetainerSlotIndex = firstRetainerIndex[toNodeIndex / nodeFieldCount];//由后向前添加,直到retainingNodes[firstRetainerSlotIndex]变为了0int nextUnusedRetainerSlotIndex = firstRetainerSlotIndex + (--retainingNodes[firstRetainerSlotIndex]);if (isValid(nextUnusedRetainerSlotIndex, retainingNodes.length) && isValid(nextUnusedRetainerSlotIndex, retainingEdges.length)) {retainingNodes[nextUnusedRetainerSlotIndex] = srcNodeIndex;retainingEdges[nextUnusedRetainerSlotIndex] = edgeIndex;}}}}}
privatevoidcalculateDistances() {for (int nodeOrdinal = 0; nodeOrdinal < nodeCount; nodeOrdinal++) {nodeDistances[nodeOrdinal] = noDistance;}int[] nodesToVisit = new int[nodeCount];int nodesToVisitLength = 0;//遍历根节点for (int edgeIndex = firstEdgeIndexes[rootNodeIndexInternal];edgeIndex < firstEdgeIndexes[rootNodeIndexInternal + 1];edgeIndex += edgeFieldsCount) {int childNodeIndex = edges[edgeIndex + edgeToNodeOffset];int childNodeOrdinal = childNodeIndex / nodeFieldCount;if (isUserRoot(childNodeIndex)) {nodeDistances[childNodeOrdinal] = 1;bfsNodes[bfsIndex++] = childNodeOrdinal;nodesToVisit[nodesToVisitLength++] = childNodeIndex;}}//从根节点进行遍历bfs(nodesToVisit, nodesToVisitLength, nodeDistances);nodeDistances[rootNodeIndexInternal / nodeFieldCount] =nodesToVisitLength > 0 ? -1 : 0;;nodesToVisit[0] = rootNodeIndexInternal;nodesToVisitLength = 1;//遍历其他单独的节点,synthetic节点bfs(nodesToVisit, nodesToVisitLength, nodeDistances);}
计算节点的Dom顺序不是采⽤先序遍历,⽽是采⽤逆后序进⾏遍历加速收敛。从基础知识那⾥可以得知dfs树有四种边,其中前向边和树边,先序遍历和逆后序遍历都是⼀次遍历就可以计算,对于返祖边,都是需要多次遍历才能计算,但对于横叉边,逆后序只需要⼀次遍历⽽先序遍历就要多次。 在计算Dom(p)的交集的朴素算法是对所有前驱节点的⽀配节点⼀⼀查找匹配,这样的效率很低很低,甚⾄可以到达O(n2)。论⽂中提出了⼀个新的⽅案,由于前驱节点的dom树已经构建完成,例如下图dom(7) = {7,1,0},dom(6) = {6,2,1,0}, dom(3) ={3,2,1,0},此时求dom(5),通过观察很容易发现dom(5)={5,1,0}。根据树的特点,求解idom(n)就转换为求解n的前驱节点在⽀配树上的公共祖先节点。

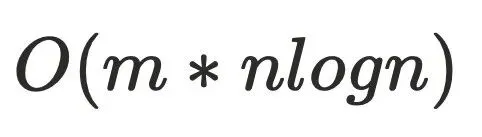 ,m是遍历次数logn是⽀配树的深度,更进⼀步,如果m是⼀个常量的话,⼀般算法复杂度可以做到
,m是遍历次数logn是⽀配树的深度,更进⼀步,如果m是⼀个常量的话,⼀般算法复杂度可以做到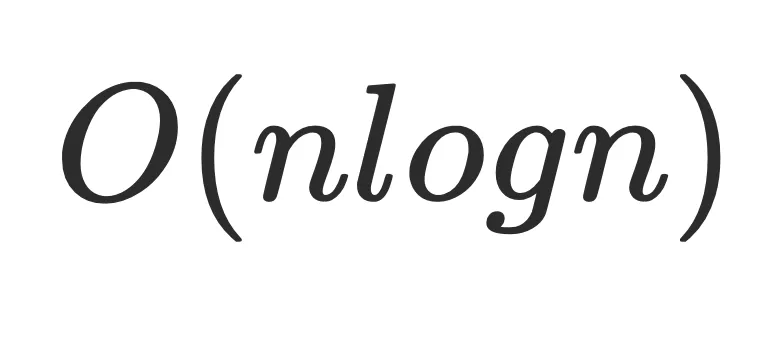 。
。voidcalculateRetainedSizes(int[] postOrderIndex2NodeOrdinal) {int postOrderIndex;for (postOrderIndex = 0; postOrderIndex < nodeCount;++postOrderIndex) {retainedSizes[postOrderIndex] = nodes[postOrderIndex *nodeFieldCount + nodeSelfSizeOffset];if (nodeNativeSizeOffset != 0) {retainedNativeSizes[postOrderIndex] = (long)nodes[postOrderIndex * nodeFieldCount + nodeNativeSizeOffset];}}//后序遍历,让被支配节点先于支配节点计算retainSizefor (postOrderIndex = 0; postOrderIndex < nodeCount - 1;++postOrderIndex) {int nodeOrdinal = postOrderIndex2NodeOrdinal[postOrderIndex];int dominatorOrdinal = 0;if (isValid(nodeOrdinal, dominatorsTree.length)) {dominatorOrdinal = dominatorsTree[nodeOrdinal];}if (isValid(dominatorOrdinal, retainedSizes.length) &&isValid(nodeOrdinal, retainedSizes.length)) {retainedSizes[dominatorOrdinal] +=retainedSizes[nodeOrdinal];if (nodeNativeSizeOffset != 0) {retainedNativeSizes[dominatorOrdinal] +=retainedNativeSizes[nodeOrdinal];}}}}
public Map<Integer, ConstructorNode> getBigHeapNode() {Map<Integer, ConstructorNode> heapNodes = new HashMap<>(nodeCount);for (int nodeOrdinal = 0; nodeOrdinal < nodeCount; nodeOrdinal++) {int nodeIndex = nodeOrdinal * nodeFieldCount;if (isHidden(nodeIndex)) {continue;}if (isSynthetic(nodeIndex)) {continue;}int stringIndex = nodes[nodeIndex + nodeNameOffset];if (heapNodes.containsKey(stringIndex)) {ConstructorNode heapNode = heapNodes.get(stringIndex);heapNode.addRetainedSize(1, retainedSizes[nodeOrdinal]);} else {String constructorName = strings.get(stringIndex);if (HarmonyAnalyzeUtils.containsTaobao(constructorName)) {ConstructorNode heapNode = new ConstructorNode(stringIndex, constructorName, 1,retainedSizes[nodeOrdinal]);heapNodes.put(stringIndex, heapNode);}}}ConfigParams configParams = CmdArgs.getInstance().getConfigParams();Map<Integer, ConstructorNode> bigNodes = new HashMap<>();for (ConstructorNode heapNode : heapNodes.values()) {if (heapNode.getRetainedSize() >= configParams.minRetainedSize || heapNode.getCount() >= configParams.minLeakCount) {bigNodes.put(heapNode.getStringIndex(), heapNode);}}return bigNodes;}
privatevoidaggregateReferenceTree() {Map<Integer, ConstructorNode> bigNodes = getTBHeapNode();//对节点进行bfsfor (int i = 0; i < bfsIndex; i++) {int nodeOrdinal = bfsNodes[i];int nodeIndex = nodeOrdinal * nodeFieldCount;int stringIndex = nodes[nodeIndex + nodeNameOffset];if (bigNodes.containsKey(stringIndex)) {Map<String, List<ConstructorNode>> referenceTrees = new HashMap<>();calculateReferenceTree(nodeOrdinal, new StringBuilder(), new ArrayList<>(), referenceTrees);for (String key : referenceTrees.keySet()) {List<ConstructorNode> refChain = referenceTrees.get(key);if (aggregatedRefTree.containsKey(key)) {ConstructorNode cached = aggregatedRefTree.get(key).get(0);//相同节点的链路不用相加if (cached == refChain.get(0)) {continue;}cached.addCount();cached.addRetainedSize(retainedSizes[nodeOrdinal]);cached.addShallowSize(nodes[nodeIndex + nodeSelfSizeOffset]);} else {if (!refChain.isEmpty()) {aggregatedRefTree.put(key, refChain);}}}}}}privatevoidcalculateReferenceTree(int nodeOrdinal, StringBuilder pathKey, List<ConstructorNode> refChain,Map<String, List<ConstructorNode>> referenceTree) {int nodeIndex = nodeOrdinal * nodeFieldCount;int stringIndex = nodes[nodeIndex + nodeNameOffset];pathKey.append(stringIndex).append('-');ConstructorNode node = new ConstructorNode(stringIndex, strings.get(stringIndex), nodeDistances[nodeOrdinal]);refChain.add(node);if (nodeDistances[nodeOrdinal] == 1) {String key = pathKey.toString();List<ConstructorNode> newRefChain = new ArrayList<>(refChain);referenceTree.put(key, newRefChain);return;}List<Integer> retainers = findRetainers(nodeOrdinal);for (Integer retainer : retainers) {StringBuilder newPathKey = new StringBuilder(pathKey);List<ConstructorNode> newRefChain = new ArrayList<>(refChain);calculateReferenceTree(retainer, newPathKey, newRefChain, referenceTree);}}


《ASimple, FastDominanceAlgorithm》: https://www.cs.tufts.edu/~nr/cs257/archive/keith-cooper/dom14.pdf
《ANew, SimplerLinear-TimeDominatorsAlgorithm》: http://adambuchsbaum.com/papers/dom-toplas.pdf
《AFastAlgorithmforFindingDominatorsinaFlowgraph》: https://faculty.cc.gatech.edu/~harrold/6340/cs6340_fall2009/Readings/lengauer91jul.pdf

本文作者灵貎,来自淘天集团-终端平台基础工程团队,团队负责淘宝App基础架构和基础链路业务,致力于通过技术创新和系统优化,打造一个更稳定、更流畅的手机淘宝。同时我们也在持续探索通过AI搭建高效、智能的研发体系,提升团队的研发效能。
